Aplicacion Problema de Pizzas: Difference between revisions
| (49 intermediate revisions by 6 users not shown) | |||
| Line 6: | Line 6: | ||
[[Image:Activity-scratch.svg]] [[Category:Aplicaciones de Actividad Scratch]] |
[[Image:Activity-scratch.svg]] [[Category:Aplicaciones de Actividad Scratch]] |
||
[[Image:Activity-socialcalc.svg]] [[Category:Aplicaciones de Actividad SocialCalc]] |
[[Image:Activity-socialcalc.svg]] [[Category:Aplicaciones de Actividad SocialCalc]] |
||
[[Image:Activity-turtleart.svg]] [[Category:Aplicaciones de Actividad TortugArte]] |
|||
[[Image:Activity-etoys.svg]] [[Category:Aplicaciones de Actividad EToys]] |
|||
[[Image:Activity-pippy.svg]] [[Category:Aplicaciones de Actividad Pippy]] |
|||
[[Category:Aplicaciones de Actividades]] |
[[Category:Aplicaciones de Actividades]] |
||
=Descripción= |
=Descripción= |
||
'''Una pizza pequeña cuesta 120 pesos. Una pizza grande cuesta 160 pesos. Gastaste 920 pesos en total. ¿Cuántas pizzas pequeñas y cuántas grandes habías comprado?''' |
|||
---- |
|||
Sí, en este caso hubo dos soluciones... si se considera que es poco probable que se compren pizzas incompletas. |
|||
Y veo que han usado tablas o gráficas para ayudarse. ¿Se necesita álgebra? |
|||
¿Han notado que haciendo tablas se pueden solucionar problemas que necesitarían álgebra? |
|||
En este caso ni con el álgebra es suficiente... de todas maneras hubo que hacer la tabla, o la gráfica. |
|||
PD. ...Y las computadoras son buenas para hacer tablas y gráficas. |
|||
==SocialCalc == |
|||
El problema tiene dos posibles soluciones, que |
|||
es facil de encontrar usando una planilla de cálculo, como el |
|||
"Socialcalc" que viene incluído en las XO. Les adjunto dicha planilla hecha en SocialCalc [[File:PIZZAS.zip]], |
|||
junto con una copia en formato excel [[File:PIZZAS.xls]]. |
|||
Seguramente se puede solucionar en forma "elegante", o "políticamente |
|||
correcta", pero para salir un poco del encasillamenito Educativo, probé |
|||
a solucionarlo de otra forma. |
|||
Usando el Socialcalc no hay que hacer elucubraciones de altas |
|||
matemáticas, es cuestión de hacer una planilla con las diferentes |
|||
posibles soluciones, por ejemplo: |
|||
1 chica, + 1 Grande |
|||
2 Chicas + 1 grande |
|||
.... |
|||
Así probás todas las posibles soluciones (hasta 10, por ej) y encontrás |
|||
en un santiamén que hay sólo dos soluciones : |
|||
* 1 Chica + 5 Grandes = 920 |
|||
* 5 Chicas + 2 Grandes = 920 |
|||
En los dos casos el gasto total es 920 |
|||
De esta forma se usa una herramienta (la XO) para solucionar un |
|||
problema, que para solucionarlo de otra forma habría que "exprimir un |
|||
poco más la materia gris", de esta forma el socialcalc nos hace el favor |
|||
de resolver el problema por nosotros. |
|||
Algunos hacen el razonamiento de que haciendo así la gente "usa menos el |
|||
cerebro" y por ende se hace más estúpida... |
|||
Es el mismo razonamiento de mucha gente del siglo pasado que obligaba a |
|||
los alumnos a no usar la calculadora... algo completamente absurdo! |
|||
En la práctica, no nos hace menos inteligentes el hecho de usar una |
|||
calculadora. Recuerdo que allá por el año 1979 yo estaba en Liceo y la |
|||
Profesora nos enseñó cómo hacer una raíz cuadrada usando lápiz y papel... |
|||
Recuerdo que yo me negué rotundamente a aprender dicho método obsoleto. |
|||
Y lo mismo hice cuando nos enseñaban alos logaritmos con las tablas! |
|||
==Scratch== |
|||
; Proyecto En-línea (requiere Java) : http://scratch.mit.edu/projects/DanielAjoy/1274051 |
|||
; Para descargar el proyecto : http://scratch.mit.edu/projects/DanielAjoy/1274051/download |
|||
[[Image:Pizzas.png|||800px]] |
|||
==Terminal== |
|||
Aprovechando la capacidad de calcular productos cartesianos [[:Category:Aplicaciones_de_Actividad_Terminal#Utilidades|mostrada aquí]]: |
|||
for i in {1,2,3,4,5,6,7,8,9,10}" "{1,2,3,4,5,6,7,8,9,10}; do echo $i; done |
|||
1 1 |
|||
1 2 |
|||
1 3 |
|||
1 4 |
|||
1 5 |
|||
1 6 |
|||
1 7 |
|||
1 8 |
|||
1 9 |
|||
1 10 |
|||
2 1 |
|||
2 2 |
|||
2 3 |
|||
... |
|||
10 1 |
|||
10 2 |
|||
10 3 |
|||
10 4 |
|||
10 5 |
|||
10 6 |
|||
10 7 |
|||
10 8 |
|||
10 9 |
|||
10 10 |
|||
Luego, queremos sólo los pares cartesianos tales que, el primer número por 120 más el segundo número por 160 den 920: |
|||
(for i in {1,2,3,4,5,6,7,8,9,10}" "{1,2,3,4,5,6,7,8,9,10}; do echo $i; done) | gawk '$1 * 120 + $2 * 160 == 920 {print}' |
|||
1 5 |
|||
5 2 |
|||
== TortugArte == |
|||
=== Solución 1 === |
|||
[[Image:TurtleArtPizza.jpg|600px]] |
|||
=== Solución 2 === |
|||
[[Image:TurtleArtPizza.png|600px]] |
|||
; Programa : [[File:ProblemaPizza.ta]] |
|||
=== Solución 3 === |
|||
; En Inglés : http://tonyforster.blogspot.com/2010/09/turtle-diophantine.html |
|||
Una solución alternativa que no se limita a 10 x 10 pizzas |
|||
[[File:Captura pantalla de "Turtle Blocks Activity Diophantine".png|600px]] |
|||
== Gráficas Online == |
|||
[http://fooplot.com/index.php?&type0=0&type1=0&type2=0&type3=0&type4=0&y0=7.666666667-1.333333333x&y1=&y2=&y3=&y4=&r0=&r1=&r2=&r3=&r4=&px0=&px1=&px2=&px3=&px4=&py0=&py1=&py2=&py3=&py4=&smin0=0&smin1=0&smin2=0&smin3=0&smin4=0&smax0=2pi&smax1=2pi&smax2=2pi&smax3=2pi&smax4=2pi&thetamin0=0&thetamin1=0&thetamin2=0&thetamin3=0&thetamin4=0&thetamax0=2pi&thetamax1=2pi&thetamax2=2pi&thetamax3=2pi&thetamax4=2pi&ipw=1&ixmin=-1&ixmax=10&iymin=-1&iymax=10&igx=1&igy=1&igl=1&igs=0&iax=1&ila=1&xmin=-1&xmax=10&ymin=-1&ymax=10 Gráfica] |
|||
== Etoys == |
|||
[[Image:EtoysPizza.png|600px]] |
|||
; Proyecto Original : http://squeakland.org/showcase/project.jsp?id=10264 |
|||
; Explicaciones del Proyecto : https://docs.google.com/View?id=dg7q79cx_823cd4vc6fw |
|||
; Proyecto Modificado : http://squeakland.org/showcase/project.jsp?id=10287 |
|||
Este proyecto es para contestar los comentarios de Pato Acevedo y de Daniel Ajoy al proyecto original How Many Pizzas. |
|||
Ellos querían ver un diagrama de flujo y querían encontrar fácilmente el código. |
|||
Esto es lo que hicimos ahora: |
|||
* Tomamos el proyecto How Many Pizzas. |
|||
* Eliminamos todo lo que no era esencial. |
|||
* Eliminamos las cuatro fotos en las esquinas. |
|||
* Eliminamos los cuatro libros que se abrían al pasar el cursor sobre las fotos. |
|||
Ahora al abrir la lista de Objetos con Guiones hay pocos objetos. |
|||
Es fácil descartar los que probablemente no tengan guiones asociados con ellos. |
|||
Se concluye así que el objeto "Tomate", es el único con guiones. |
|||
Abrimos el visor de ese objeto y vemos que tiene los guiones y las variables." |
|||
==Pippy== |
|||
[[File:Captura pantalla de "Pippy Activity pizza".png|600px]] |
|||
=Faltantes= |
|||
Faltarían soluciones en: |
|||
* Calculator |
|||
* Javascript |
|||
* Otras maneras?? |
|||
=Modificaciones= |
|||
== Juguetes == |
|||
Pepe está a cargo de una fundación y para Navidad compró dos tipos de juguetes, los baratos costaron $11 cada uno y los caros $17. En total compró $1000. ¿Cuántas juguetes baratos y caros compró? |
|||
=== Problema planteado por J.B.Búa a sus alumnos === |
|||
En [http://centros.edu.xunta.es/iesramoncabanillas/cuadmat/index.htm su página]. El problema se propuso a los alumnos, sin más comentarios o indicaciones. |
|||
* [http://centros.edu.xunta.es/iesramoncabanillas/cuadmat/trabaj/andrea.pdf Trabajo de Andrea Franco Carballa (pdf)] |
|||
* [http://centros.edu.xunta.es/iesramoncabanillas/cuadmat/trabaj/marcos.pdf Trabajo de Marcos Horro Varela (pdf)] |
|||
* [http://centros.edu.xunta.es/iesramoncabanillas/cuadmat/trabaj/noelia.pdf Trabajo de Noelia Vieites Parada (pdf)] |
|||
== Hamburguesas == |
|||
Una hamburguesa pequeña cuesta 2 dólares. Una hamburguesa grande cuesta 3 dólares. Gasté $24 dólares en total. Cuántas hamburguesas pequeñas y cuántas grandes compré? |
|||
=Aportan= |
=Aportan= |
||
* Daniel Ajoy |
* Daniel Ajoy |
||
* alfonsotissoni |
|||
* Walter López |
|||
* Paolo Benini |
|||
* Carlos Rabassa |
|||
* Tony Forster |
|||
* J.B.Búa |
|||
Latest revision as of 14:47, 22 November 2010
Nivel
???
Actividades
Descripción
Una pizza pequeña cuesta 120 pesos. Una pizza grande cuesta 160 pesos. Gastaste 920 pesos en total. ¿Cuántas pizzas pequeñas y cuántas grandes habías comprado?
Sí, en este caso hubo dos soluciones... si se considera que es poco probable que se compren pizzas incompletas.
Y veo que han usado tablas o gráficas para ayudarse. ¿Se necesita álgebra?
¿Han notado que haciendo tablas se pueden solucionar problemas que necesitarían álgebra?
En este caso ni con el álgebra es suficiente... de todas maneras hubo que hacer la tabla, o la gráfica.
PD. ...Y las computadoras son buenas para hacer tablas y gráficas.
SocialCalc
El problema tiene dos posibles soluciones, que es facil de encontrar usando una planilla de cálculo, como el "Socialcalc" que viene incluído en las XO. Les adjunto dicha planilla hecha en SocialCalc File:PIZZAS.zip, junto con una copia en formato excel File:PIZZAS.xls.
Seguramente se puede solucionar en forma "elegante", o "políticamente correcta", pero para salir un poco del encasillamenito Educativo, probé a solucionarlo de otra forma.
Usando el Socialcalc no hay que hacer elucubraciones de altas matemáticas, es cuestión de hacer una planilla con las diferentes posibles soluciones, por ejemplo:
1 chica, + 1 Grande 2 Chicas + 1 grande ....
Así probás todas las posibles soluciones (hasta 10, por ej) y encontrás en un santiamén que hay sólo dos soluciones :
- 1 Chica + 5 Grandes = 920
- 5 Chicas + 2 Grandes = 920
En los dos casos el gasto total es 920
De esta forma se usa una herramienta (la XO) para solucionar un
problema, que para solucionarlo de otra forma habría que "exprimir un
poco más la materia gris", de esta forma el socialcalc nos hace el favor
de resolver el problema por nosotros.
Algunos hacen el razonamiento de que haciendo así la gente "usa menos el cerebro" y por ende se hace más estúpida...
Es el mismo razonamiento de mucha gente del siglo pasado que obligaba a los alumnos a no usar la calculadora... algo completamente absurdo!
En la práctica, no nos hace menos inteligentes el hecho de usar una calculadora. Recuerdo que allá por el año 1979 yo estaba en Liceo y la Profesora nos enseñó cómo hacer una raíz cuadrada usando lápiz y papel... Recuerdo que yo me negué rotundamente a aprender dicho método obsoleto. Y lo mismo hice cuando nos enseñaban alos logaritmos con las tablas!
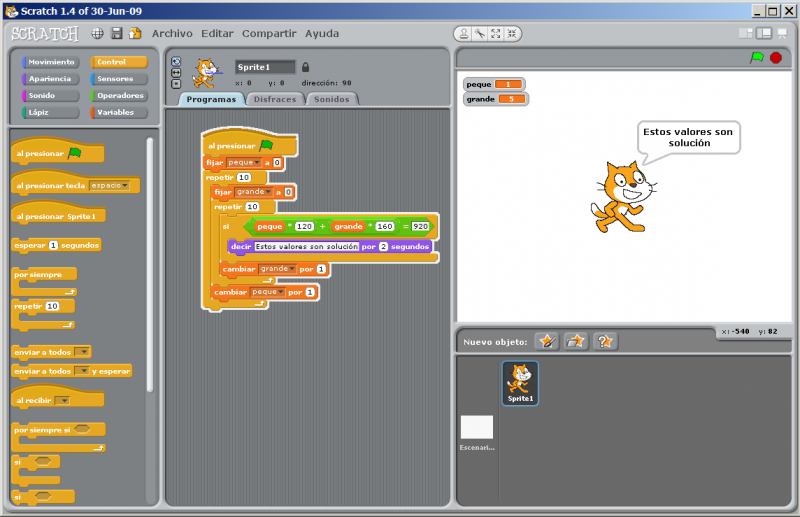
Scratch
- Proyecto En-línea (requiere Java)
- http://scratch.mit.edu/projects/DanielAjoy/1274051
- Para descargar el proyecto
- http://scratch.mit.edu/projects/DanielAjoy/1274051/download
Terminal
Aprovechando la capacidad de calcular productos cartesianos mostrada aquí:
for i in {1,2,3,4,5,6,7,8,9,10}" "{1,2,3,4,5,6,7,8,9,10}; do echo $i; done
1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 10 2 1 2 2 2 3 ... 10 1 10 2 10 3 10 4 10 5 10 6 10 7 10 8 10 9 10 10
Luego, queremos sólo los pares cartesianos tales que, el primer número por 120 más el segundo número por 160 den 920:
(for i in {1,2,3,4,5,6,7,8,9,10}" "{1,2,3,4,5,6,7,8,9,10}; do echo $i; done) | gawk '$1 * 120 + $2 * 160 == 920 {print}'
1 5 5 2
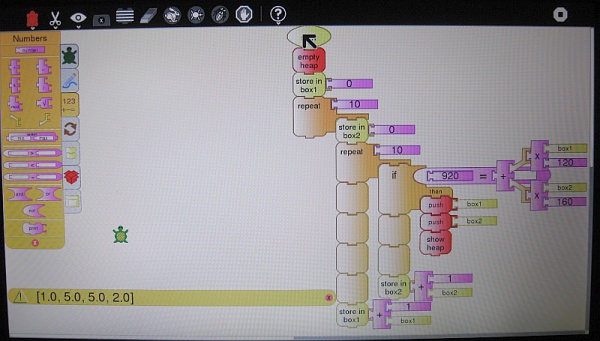
TortugArte
Solución 1
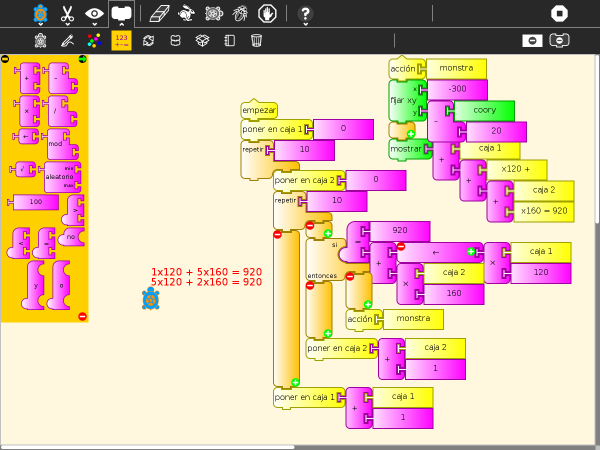
Solución 2
- Programa
- File:ProblemaPizza.ta
Solución 3
Una solución alternativa que no se limita a 10 x 10 pizzas
Gráficas Online
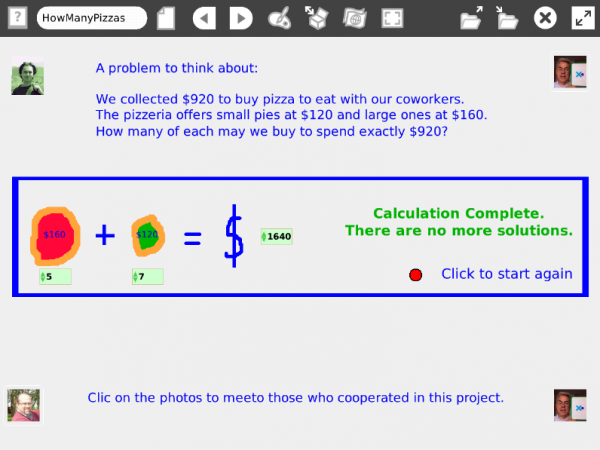
Etoys
- Proyecto Original
- http://squeakland.org/showcase/project.jsp?id=10264
- Explicaciones del Proyecto
- https://docs.google.com/View?id=dg7q79cx_823cd4vc6fw
- Proyecto Modificado
- http://squeakland.org/showcase/project.jsp?id=10287
Este proyecto es para contestar los comentarios de Pato Acevedo y de Daniel Ajoy al proyecto original How Many Pizzas.
Ellos querían ver un diagrama de flujo y querían encontrar fácilmente el código.
Esto es lo que hicimos ahora:
- Tomamos el proyecto How Many Pizzas.
- Eliminamos todo lo que no era esencial.
- Eliminamos las cuatro fotos en las esquinas.
- Eliminamos los cuatro libros que se abrían al pasar el cursor sobre las fotos.
Ahora al abrir la lista de Objetos con Guiones hay pocos objetos.
Es fácil descartar los que probablemente no tengan guiones asociados con ellos.
Se concluye así que el objeto "Tomate", es el único con guiones.
Abrimos el visor de ese objeto y vemos que tiene los guiones y las variables."
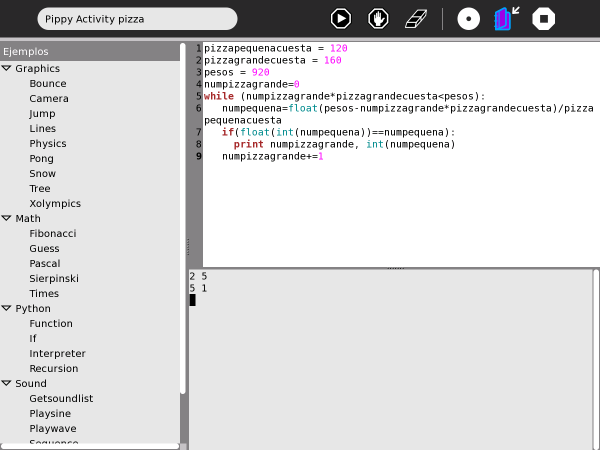
Pippy
Faltantes
Faltarían soluciones en:
- Calculator
- Javascript
- Otras maneras??
Modificaciones
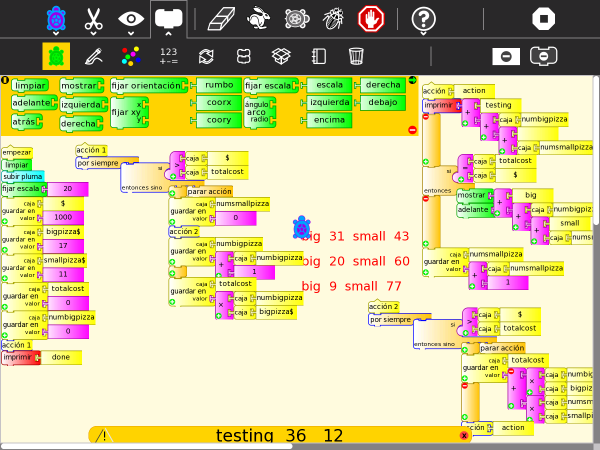
Juguetes
Pepe está a cargo de una fundación y para Navidad compró dos tipos de juguetes, los baratos costaron $11 cada uno y los caros $17. En total compró $1000. ¿Cuántas juguetes baratos y caros compró?
Problema planteado por J.B.Búa a sus alumnos
En su página. El problema se propuso a los alumnos, sin más comentarios o indicaciones.
- Trabajo de Andrea Franco Carballa (pdf)
- Trabajo de Marcos Horro Varela (pdf)
- Trabajo de Noelia Vieites Parada (pdf)
Hamburguesas
Una hamburguesa pequeña cuesta 2 dólares. Una hamburguesa grande cuesta 3 dólares. Gasté $24 dólares en total. Cuántas hamburguesas pequeñas y cuántas grandes compré?
Aportan
- Daniel Ajoy
- alfonsotissoni
- Walter López
- Paolo Benini
- Carlos Rabassa
- Tony Forster
- J.B.Búa