Sugar Etoys/lang-ko
환영합니다 | Portal | XO Korea | Deployment | Content | Hardware | Software | Mesh Network | Ethics | LOS | XO City | Accreditation | Consortium
Contents
BTest OLPC XO 2006년 11월 Build 스퀵 이토이
2006년 11월 이후로 내용이 추가 중인 문서입니다..
OLPC XO 이토이
| EToys | |
| Status: | unknown |
| Version: | unknown |
| Base: | Yes |
| Source: | unknown |
| l10n: | missing |
| Contributors | |
| unknown | |
BTest 빌드를 위한 이 실험적 시스템은 XO 상에서 광범위한 테스트를 거쳤는데, 스크린 사이즈와 가독성, 사운드 및 동적 그래픽 생성, 카메라 이용, 키보드, 태블릿 (특히, 페인팅과 포인팅), 외부 장치 (물리적 세계 센서), 협업과 멘터링 등을 포함힙니다. 향후 어른들의 도움없이 어린이 스스로 학습할 수 있는 인터페이스와 자료를 제공하기 위한 광범위한 시도가 진행될 것입니다.
Viewpoints Research Institute는 여러분의 참여를 기대합니다. XOetoys@squeakland.org
This experimental system for the BTest build was done to test a wide range of Etoys facilities on the XO, including: screen size and legibility, sound and dynamic graphics generation, use of the camera, keyboard, and tablet (especially for painting and pointing), external devices (such as physical world sensors), collaboration & mentoring, etc. One of the main new facilities supplied here that will be fleshed out considerably in future builds is a comprehensive attempt to provide an interface and material that can help children learn Etoys without requiring expert adults to help them.
This document will cover the Etoys facilities provided in this experimental build, and we at Viewpoints Research Institute (a nonprofit research organization devoted to helping children learn to think), invite users and testers to email us with comments, questions and complaints at XOetoys@squeakland.org .
BTest-1 이토이 버전의 상태
향후, 우리는 가능한 슈가 UI 협약을 따르는 인터페이스를 제작할 것인데, XO의 높은 해상도, 특별한 컬러 표현은 새로운 디자인, 폰트, 리사이징 등을 요구합니다. XO의 낮은 동작 속도로 인해, 코드 최적화와 간소화 역시 요구됩니다.
현재 버전은 일반적으로 배포되는 표준 다국어 시스템입니다.
We plan to make the Etoys user interface use as many of the OLPC "Sugar" UI conventions as possible. The latter are still being designed, so there is currently not a lot of coherence with Sugar, and Etoys thus uses its own UI conventions (which are explained below). The very high resolution and unusual color gamut of the XO display required some new design, fonts, resizing, etc. The slower speed of the XO required some optimizations and a few simplifications.
This version of Etoys was adapted from the standard multilingual system that is already used in many places in the world (and is discussed at Squeakland Website and in the book Powerful Ideas in the Classroom by B.J. Allen-Conn and Kim Rose. For convenience, we will give a gist of this material here using screen shots from the actual XO Etoys version and examples on the BTest-1 machine.
이토이 소개
이토이는 특히 어린이를 위한 저작 시스템이며, 다양한 다이나믹 미디어들이 만들어지고, 프로그램되며, 스크립트되어, 공유 및 협업을 지원합니다. 특히 과학과 수학 학습을 위한 도구로 활용되고 있습니다.
이토이의 탄생에 영향을 미친 언어들로는 로고, 스몰토크, 하이퍼카드, 그리고 스타로고입니다. 12살 아동을 주된 초점으로 제작되었지만, 더 어리거나, 더 큰 청소년들에게도 적합합니다. 현재, 글을 읽지 못하는 유아들과 복잡한 프로그래밍 기능을 요구하는 성인들 모두를 지원하기 위한 개발 작업을 진행하고 있습니다.
이토이는 1998년 이후 무료로 사용가능하며, 플랫폼 독립적입니다. 이토이는 독일어, 불어, 스페인어, 일본어, 한국어, 중국어, 스와힐리어 등으로 현지화되어 있습니다.
Squeakland 사이트에 다양한 자료가 올라가 있습니다.
Etoys is an authoring system, primarily aimed at children, in which a wide variety of dynamic media can be created and programmed/scripted, shared and collaborated. Much of the use of Etoys has been as a vehicle to help children learn "powerful ideas", especially in science and mathematics.
The main ancestors and influences of Etoys were Logo, Smalltalk, Hypercard, and StarLogo. This version was designed primarily for 9–12 year olds, but has been used successfully with younger and older children. We are in the process of making a multiple user-interface system that will better cater to the needs of young children (especially those who don't yet read) and older children who can handle many more operations and complex planning.
Etoys has been freely available on the Internet since 1998 and works on all the standard platforms (and many nonstandard ones). Etoys is localizable, and there are versions in German, French, Spanish, Japanese, Korean, Chinese, Swahili, etc. The Etoys home website is web address of Squeakland , and this contains quite a bit of material about the use of Etoys, the philosophy of education employed, and many examples done by children, teachers, and parents. Etoys is currently in more than a dozen countries and has been quite successful.
이토이 미디어
이토이는 스크립트 가능한 미디어 오브젝트를 가지며, 어린이들이 더 만들 수 있습니다. 긎 ㅜㅇ에는 드로잉과 페인팅, 텍스트 (광범위한 레이아웃 기능 포함), 픽처 (BMP, JPEG, GIF, PNG), 애니메이션, 무비 (MPEG), 사운드 (MP3), 사운드 레코더, 사운드 신스시스 (샘플링, FM 등), 미디 플레이어와 에디터, 북(하이퍼카드 스택과 비슷함), 풍부한 기능의 웹 페이지 등이 포함됩니다. 이 모두는 WYSIWYG (what you see is what you get)를 지원하며, 직접 조작과 스크립팅을 통한 저작을 지원합니다.
Etoys has many scriptable media objects, and the children can create more. These include: drawings & paintings, text (including ability to do extensive layouts), pictures (BMP, JPEG, GIF, PNG), animations, movies (MPEG), sound (MP3), sound recorders, sound synthesis (sampling, FM, etc.), MIDI player and editor, "books" (like Hypercard stacks), enriched webpages, etc. These are all WYSIWYG (what you see is what you get) intermixable and authorable via direct manipulation and scripting.
이토이의 교육적 용도
이토이는 Seymour Papert, Piaget, Montessori, Dewey, Vygotsky, 그리고 Jerome Bruner의 교육 사상을 담고 있습니다. 기본 이론은, 생각을 kinesthetically, 시각적, 청각적, 그리고 상징적으로 마주하고, 더불어 놀며, 구성하는 경험을 통한 학습이 어린이들에게 최선이라는 생각입니다. 이러한 경험이 어린이들의 인지 능력의 발달 단계에 부합할 때 더욱 효과적이라는 주장이 곧잘 함께 합니다.
가령, 계산이란 변화가 시간 및 공간적 속성으로 표현 가능한 점진적 과정이라는 생각에 기초합니다. 이러한 "변화의 수학"은 흔히 대수학적인 기호와 기하학으로 표현되며, 어린이들이 중고등학교에 진학한 뒤에 정규적으로 배우게 됩니다.
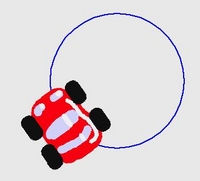
그러나, 페퍼트는 어린이들이 이미 변화의 세계 속에 살고 있고, 그것을 이해하고 있는데, 특히 몸을 움직이거나, 간단한 계획을 세우는 등의 과정에서 그들이 본능적으로 깨우치고 있는 "변화의 수학"에 대한 이해를 적용하고 있다고 생각합니다. 가령, 원의 수학적 표현식을 위해 수학 방정식을 익히는 대신, 어린이들은 앞으로 조금가고, 옆으로 약간 옮긴 뒤, 다시 앞으로 조금가는 과정을 반복함으로써 원을 그릴 수 있음을 경험을 통해 쉽게 배울 수 있습니다.
원 속에 걷고 있는 어린이
이토이는 이것을 작은 시계 아이콘으로 작동되는 스크립트로 표현합니다.
사실,어린이들은 (흔히 그림의 형태로) 스크린 상에 무언가를 창조하고, 이토이가 실행할 간단한 스크립트로 그것에 생명을 불어넣는데, 이 것은 그들이 배워야 할 것으로 우리가 기대하는 수학적 원리들을 그들이 자연스럽게 익혀 나가는 과정이 됩니다.
In practice, the children first make something on the screen (usually by painting a picture), then they bring their creation to life by writing simple scripts that are both directions to Etoys for actions to be done and they are mathematical expressions of change in this special version of the calculus that we are helping them learn.
이토이의 모든 오브젝트는 펜을 가지는데, 이토이는 "옷을 입을 수 있는 무수한 거북이를 가진 로고"로 표현될 수 있습니다.
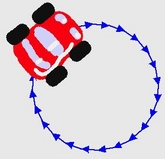
Every object in Etoys also has a pen, so one way to think of Etoys is "Logo with unlimited Turtles that can wear Costumes". We can use the pen to help us reflect on dynamic changes. For example, we can reveal the vector nature of a circle by choosing to have arrows drawn instead of just lines. Or we can make it easier to see the distances of the "hops" by drawing dots. Another way to think of the "distances of the hops" is a measure of the speed of the car (since each hop is taken on a uniform tick of the script, and "speed" is the distance traveled in some unit of time). The script shows this also as the units the car moves forward (in this case, it is 5).
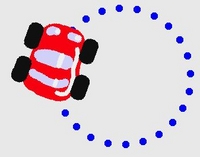
스피드와 가속에 대해 좀더 자세히 살펴보면, 아래 스크립트는 자동차를 매 순간 30 유닛만큼 움직입니다. "점을 찍는" 펜을 작동함으로써, 자동차 뒤에 일정하게 30 유닛의 공간이 표시됨을 볼 수 있습니다. "거리의 변화"가 속도이며, 여기서 우리는 속도가 일정함을 알 수 있습니다.
예 1
속도를 일정하게 증가시키는 (가령 20) 스크립트를 더하면, 찍혀지는 점들의 간격이 점차 넓어지는 것을 볼 수 있는데, 각각이 20씩 넓어집니다. "속도의 변화"는 가속이며, 우리는 자동차가 가속하고 있음을 알 수 있습니다 (20의 비율로 일정하게).
예 2
재미난 오브젝트를 만들고, 동적인 변화를 추가함으로써, 중요한 수학적 원리들을 깊이있게 이해할 수 있게 됩니다. 과학은 세상을 관찰함으로써 정보를 얻습니다. XO의 카메라를 이용하여, 떨어지는 물체와 같은 친숙한 현상을 가까이 관찰할 수 있습니다. 이토이는 개별 프레임이 늘여지고, 비교될 수 있도록 합니다.
무비와 프레임
무비 프레임을 포갬으로써, 공이 일정한 속도로 움직이지 않음을 알 수 있습니다. 따라서, 우리는 공이 가속 중임을 알 수 있습니다. 공급 빈에서 사각형을 가져와 공들 간의 거리를 측정할 수 있습니다.
거리 측정
그 다음 이 사각형들을 포개봅니다. 항상 일정한 비율로 크기가 증가함을 곧바로 볼 수 있습니다! (여기서 우우우와아아php5하고..^^). 이를 통해, 어린이들은 자동차의 경우와 마찬가리의 스크립트를 신속히 작성할 수 있게 죄지만, 이번에는 수직적인 공의 이동입니다.
공의 가속 스크립트
11살 어린이의 말입니다.: 머라머라... 누가 좀 번역하셈
Let's look closer at speed and acceleration. The following script will always move the car by thirty screen units on each tick. We have turned the pen inking to "make dots", and these are left behind spaced uniformly 30 screen units apart just as the script says. "Change of distance" is called speed (or velocity) and we can see here that the speed is constant.
Example one
Now let's write a script to change the speed by a constant amount (say 20). This is what "increase by" does, and we see the result with the dots spaced wider and wider apart. If we measure, we see that each are 20 wider than the previous dot spacing. "Change of speed" is called "acceleration" and we can see that the car is accelerating (and at a constant acceleration of 20).
Example two
Much important mathematics can be learned very deeply by making interesting objects and getting them to make dynamic changes. Science has to look at the world for information (because we've found that human attempts to just think about the world result in stories that rarely are in accord with what the world actually does). We can use the camera on the XO to look more closely at familiar phenomena, such as falling objects. Etoys allows individual frames to be pulled out and compared.
Movie and frames
If we stack up the movie frames, we can see that the ball is not traveling at a constant speed (if it were the ball images would be spaced evenly apart, as they were in the above example about constant speed). Instead, they are spaced further and further apart, so we can easily see that they are accelerating. If we get rectangles from our supply bin, we can use them to measure the distance between each image of the ball by stretching them until they reach from the bottom of the ball image on one frame to the bottom of the ball image on the next frame. This distance is a measure of the speed of the ball (because it is the distance traveled in the constant time between frames of the movie).
Measuring the distances
Now we can move the rectangles over themselves to see what the changes in speed actually were. They look quite constant! Each rectangle has about the same increase of height as the one before it. This change is the acceleration (because it is the change of the speed) and it looks quite constant. This allows the child to quickly write a script that is just like the one they wrote for the car above, but this time changing the vertical location of the ball.
The acceleration script for the ball
Here is what an 11 year old child had to say about his project: And to make sure that I was doing it just right, I got a magnifier which would help me figure out if I had it - if the size was just right. After I'd done that I would go and click on the little basic category button and then a little menu would pop up and one of the categories would be Geometry, so I clicked on that. And here it has many things that have to do with the size and shape of the rectangle. So I would see what the height is… I kept going along the process until I had them all lined up with their height. I subtracted the smaller one's height from the bigger one to see if there was a kind of pattern anywhere that could help me out. And my best guess worked: so in order to show that it was working, I decided to make – to leave – a dot copy (so that it would show that the ball was going at the exact right speed. And acceleration. )
He wanted to see if his model really did follow what the real world did, and to determine this, decided to make his simulated ball drop a dot like the car he had done previously. By playing around with the constant of acceleration, he soon found the one that modeled the acceleration of gravity in the real world and was able to confirm that his mathematical model derived from the movies of a ball dropping in the physical world matched up very well (Newton would have said "Pretty nearly") with the physical evidence. Thus, this child (and all the other children in this class) was able to undergo a complete scientific experience (very like what Galileo did about 400 years ago). This should be contrasted with the experience in most American colleges, where it has been shown that about 70% of the college students fail to understand Galilean gravity. The college approach often doesn't use calculus and also usually just gives the students the algebraic equations that they are supposed to verify by experiment. The very different approach here uses a discrete additive model for change ("increase by") that is very intuitive for all ages, and the children actually derive the relationships from the evidence. This would almost certainly also work much better in college than the way it is generally done now.
{Newton's later theory shows that this model is off by about one part in a million near the surface of the Earth. And Einstein's much later theory shows that Newton's theory is off by the tiniest fraction of a degree per century for planets near the Sun. Recent studies in cosmology seem to indicate that Einstein's theory might be off by a little, etc. This is an excellent illustration that good scientific theories are like good maps, very accurate but with some errors. This is the aim of science: total Truth in the mathematical sense is probably not possible, but tremendously accurate and useful "maps" (represented usually in mathematics) of physical phenomena can be found.}
프리젠테이션과 공유
어린이들이 프로젝트에 이용하는 "데스크탑"은 인터넷으로 전송 가능한 웹페이지이며, 서버나 웹 사이트에 저장될 수 있으며, 브라우저로 검색 및 다운로드 가능합니다. 이토이는 무수한 "프로젝트/테스크탑"을 가지며, 이를 통해 실험을 손쉽게 표현할 수 있습니다. 프로젝트/데스크탑은 분류되고, 정렬되므로, 추가적인 어플리케이션 (파워포인트 등)이 필요하지 않습니다.
The "desktop" that the children used to do their projects is also (automatically) an enriched webpage that can be sent around the Internet, put on servers and websites, and found and downloaded via browsers. Etoys has an unlimited number of these "project/desktops" and this provides a convenient way to turn experiments into presentations. The project/desktops can be sorted and shown one after another, so no additional applications (such as powerpoint) are needed.
이토이 레퍼런스
스퀵 이토이 레퍼런스 또는 이토이 컨트롤를 참조하십시오.
XO에서 이토이 시작하기
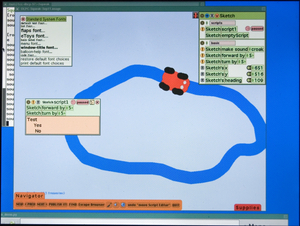
전형적 이토이 월드
이토이 프로젝트 세트.
네비게이터 탭
네비게이터 탭 ![]() 을 클릭하면, 네비게이터 플랩을 열 수 있습니다.
을 클릭하면, 네비게이터 플랩을 열 수 있습니다.
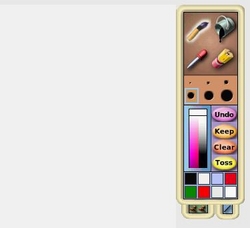
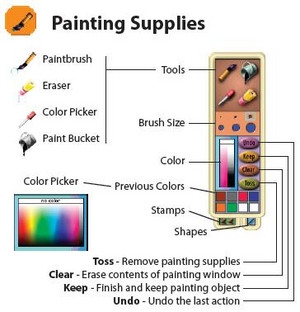
![]() 페이트 붓 아이콘은 페인팅 팔레트와 페인트 영역을 보여줍니다.
페이트 붓 아이콘은 페인팅 팔레트와 페인트 영역을 보여줍니다.
페인팅
페인팅 영역은 손쉬운 추적을 지원하며, 어떤 그림이 그려지고 있는지 선명하게 보여줍니다. 이 영역은 표준 이토이 오브젝트이며 이동, 크기 조절, 컬러 변화가 가능하고 (Graphical Properties Sheet 참조), 페인팅 영역이 화면을 가득 채울 수도 있습니다.
The painting area is normally set to be translucent to allow easy tracing and to make it very clear just what is being painted. This area is a standard Etoy object and can be moved, scaled, and colored in various ways (see Graphical Properties Sheet). There is a Preference that can choose to have the painting area be the entire size of the screen.